TCP重传机制
TCP要保证所有的数据包都可以到达,所以,必需要有重传机制。
注意,接收端给发送端的 ack 确认只会确认最后一个连续的包,比如,发送端发了 1,2,3,4,5 一共五份数据,接收端收到了1,2,于是回ack 3,然后收到了4(注意此时3没收到),此时的TCP会怎么办?我们要知道,因为正如前面所说的,SeqNum和Ack是以字节数为单位,所以 ack 的时候,不能跳着确认,只能确认最大的连续收到的包,不然,发送端就以为之前的都收到了。
超时重传机制
一种是不回 ack,死等3,当发送方发现收不到3的 ack 超时后,会重传3。一旦接收方收到3后,会 ack 回 4——意味着3和4都收到了。
但是,这种方式会有比较严重的问题,那就是因为要死等3,所以会导致4和5即便已经收到了,而发送方也完全不知道发生了什么事,因为没有收到 ack,所以,发送方可能会悲观地认为也丢了,所以有可能也会导致4和5的重传。
对此有两种选择:
一种是仅重传
timeout的包。也就是第3份数据。另一种是重传
timeout后所有的数据,也就是第3,4,5这三份数据。
这两种方式有好也有不好。第一种会节省带宽,但是慢,第二种会快一点,但是会浪费带宽,也可能会有无用功。但总体来说都不好。因为都在等 timeout,timeout 可能会很长(在下篇会说TCP是怎么动态地计算出 timeout 的)
快速重传机制
于是,TCP引入了一种叫 Fast Retransmit 的算法,不以时间驱动,而以数据驱动重传。也就是说,如果,包没有连续到达,就 ack 最后那个可能被丢了的包,如果发送方连续收到3次相同的 ack,就重传。Fast Retransmit 的好处是不用等超时了再重传。
比如:如果发送方发出了1,2,3,4,5份数据,第一份先到送了,于是就 ack 回2,结果2因为某些原因没收到,3到达了,仍然 ack 回2,后面的4和5都到了,也仍然 ack 回2,因为2还是没有收到,于是发送端收到了三个 ack=2 的确认,知道了2还没有到,于是就马上重传2。然后,接收端收到了2,此时因为3,4,5都收到了,于是 ack 回6。示意图如下:

Fast Retransmit 只解决了一个问题,就是 timeout 的问题,它依然面临一个艰难的选择,就是,是重传之前的一个还是重传所有的问题。对于上面的示例来说,是重传#2呢还是重传#2,#3,#4,#5呢?因为发送端并不清楚这连续的3个 ack(2) 是谁传回来的?也许是#6,#10,#20传来的,这样发送端很有可能要重传从2到20的这堆数据(这就是某些 TCP 的实际的实现)。可见,这是一把双刃剑。
SACK 方法
另外一种更好的方式叫:Selective Acknowledgment (SACK)(参看RFC 2018),这种方式需要在 TCP 头里加一个 SACK 的东西,ACK 还是 Fast Retransmit 的 ACK,新增的 SACK 用于汇报已收到的数据段。参看下图:

这样,在发送端就可以根据回传的 SACK 来知道哪些数据到了,哪些没有到。于是就优化了 Fast Retransmit 的算法。当然,这个协议需要两边都支持。在 Linux 下,可以通过 tcp_sack 参数打开这个功能(Linux 2.4 后默认打开)。
注意1:接收方有权把已经报给发送端 SACK 里的数据给丢了。因此不能用 SACK 完全代替 ACK,ACK 仍然需要保留。
注意2:SACK 会消费发送方的资源,试想,如果一个攻击者给数据发送方发一堆 SACK 的选项,这会导致发送方开始要重传甚至遍历已经发出的数据,这会消耗很多发送端的资源。详细的东西请参看《TCP SACK的性能权衡》
Duplicate SACK / D-SACK
有时候接收端收到数据了,但是返回的 ACK 丢了 / 超时到达。发送端没有收到 ACK,以为丢包了,就会重传。这种重传其实是没必要的。
因此有了 Duplicate SACK ,又称 D-SACK。从上面可以看到,SACK 是一个区间数组,如果这个数组的第一个区间被 ACK 覆盖,或者被第二个区间包含,就是 D-SACK 的做法,表示收到的数据之前传过了,是重复的数据,不需再传了。
超时时长的设置
TCP的RTT算法
从前面的 TCP 重传机制我们知道 Timeout 的设置对于重传非常重要。
设长了,重发就慢,丢了老半天才重发,没有效率,性能差
设短了,会导致可能并没有丢就重发。于是重发的就快,会增加网络拥塞,导致更多的超时,更多的重发。
而且,这个超时时间在不同的网络的情况下,根本没有办法设置一个死的值,只能动态地设置
为了动态地设置,TCP 引入了 RTT: Round Trip Time,也就是一个数据包从发出去到回来的时间。这样发送端就大约知道需要多少的时间,从而可以方便地设置 RTO (Retransmission TimeOut),以让我们的重传机制更高效。 听起来似乎很简单,好像就是在发送端发包时记下 t0,然后接收端再把这个 ack 回来时再记一个 t1,于是 RTT = t1 – t0。没那么简单,这只是一个采样,不能代表普遍情况。
总体思路是:超时时间 = 较大权重 × 最近几次 RTT + 较小权重 + 稍远几次的 RTT
经典算法
RFC793 中定义的经典算法是这样的:
1)首先,先采样 RTT,记下最近好几次的 RTT 值。
2)然后做平滑计算 SRTT((Smoothed RTT)。公式为:
其中的 α 取值在0.8 到 0.9之间,这个算法英文叫 Exponential weighted moving average,中文叫加权移动平均
3)开始计算 RTO。公式如下:
其中:
UBOUND是最大的timeout时间,上限值LBOUND是最小的timeout时间,下限值β 值一般在1.3到2.0之间。
Karn / Partridge 算法
但是上面的这个算法在重传的时候会出有一个终极问题——你是用第一次发数据的时间和 ACK 回来的时间做 RTT 样本值,还是用重传的时间和 ACK 回来的时间做RTT样本值?
这个问题无论你选那头都是按下葫芦起了瓢。 如下图所示:
情况(a)是
ACK没回来,所以重传。如果你计算第一次发送和ACK的时间,那么,明显算大了。情况(b)是
ACK回来慢了,但是导致了重传,但刚重传不一会儿,之前ACK就回来了。如果你是算重传的时间和ACK回来的时间的差,就会算短了。
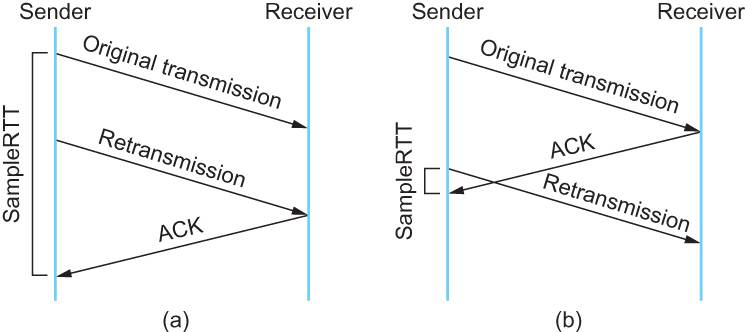
所以1987年的时候,搞了一个叫Karn / Partridge Algorithm,这个算法的最大特点是——忽略重传,不把重传的RTT做采样(你看,你不需要去解决不存在的问题)。
但是,这样一来,又会引发一个大BUG——如果在某一时间,网络闪动,突然变慢了,产生了比较大的延时,这个延时导致要重转所有的包(因为之前的RTO很小),于是,因为重转的不算,所以,RTO就不会被更新,这是一个灾难。 于是Karn算法用了一个取巧的方式——只要一发生重传,就对现有的 RTO 值翻倍(这就是所谓的 Exponential backoff),很明显,这种死规矩对于一个需要估计比较准确的RTT也不靠谱。
Jacobson / Karels 算法
前面两种算法用的都是“加权移动平均”,这种方法最大的毛病就是如果RTT有一个大的波动的话,很难被发现,因为被平滑掉了。所以,1988年,又有人推出来了一个新的算法,这个算法叫 Jacobson / Karels Algorithm(参看RFC6289)。这个算法引入了最新的 RTT 的采样和平滑过的 SRTT 的差距做因子来计算。 公式如下:(其中的DevRTT是Deviation RTT的意思)
计算平滑RTT
计算平滑RTT和真实的差距(加权移动平均)
神一样的公式
在 Linux 下,α = 0.125,β = 0.25, μ = 1,∂ = 4。这就是算法中的“调得一手好参数”,(nobody knows why, it just works…)
最后的这个算法在被用在今天的TCP协议中(Linux的源代码在:tcp_rtt_estimator)。
参考
Last updated